Pythonでグラフ(指数関数、シグモイド関数、対数関数)
2022/3/22 2022/4/15

Pythonを使ったデータ分析の勉強を始めました。
Pythonを使ったデータ分析には、Pythonを使う力&データを分析する力(統計の知識&数学の知識)が必要です。高校生時代に勉強しなかった微分・積分の知識も含まれ、趣味と思ってのんびり勉強してます。
今回は、Pythonを使ってデータ分析の考え方に必要な基礎的な関数を描いていこうと思います。
指数関数
以下のように、〇乗といった式です。累乗とかべき乗と言いますね。
$$f(x) = 2^x$$
実際にJupyter Notebookで描いてみます。なお、データ分析ではネイピア数eを底とする関数が良く使われるそうなので、以下の関数を描画します。
$$f(x) = e^x$$
import matplotlib.pyplot as plt
import numpy as np
import math
x = np.arange(-5, 6, 1)
y = float(math.e) ** x
plt.plot(x, y, label="f(x)=e^x")
plt.legend()
plt.showこのようなグラフができます。
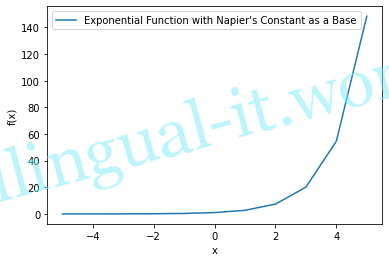
特徴として、
- x=1の時、f(x)=1となる。※数の1乗は常に1のため
- xが大きくなるにつれf(x)は急激に増え、小さくなると0に近づく
少しだけ英語の勉強もしておくと、
- Exponential Function:指数関数
- Napier’s Constant:ネイピア数
- Base:指数関数等の底
シグモイド関数
指数関数を応用しており、Deep Learningの基礎的技術であるニューラルネットワークで良く使われる、らしいです。
$$f(x) = \frac{1}{1+e^{-x}}$$
まだどう使うのか私は分かりませんが、練習のため、描画してみます。
import matplotlib.pyplot as plt
import numpy as np
import math
x = np.arange(-10, 10, 1)
e = math.e
y = 1 / (1 + e ** (-x) )
plt.plot(x, y, label="Sigmoid Function")
plt.title("Sigmoid Function")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.grid()
plt.legend
plt.show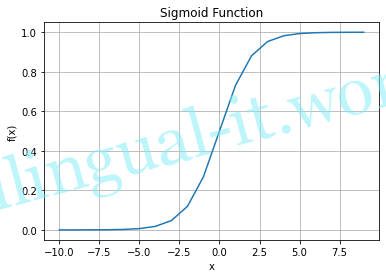
対数関数
入力された値が底の何乗に相当するかを出力します。
$$f(x) = \log_2 x$$
例えば、f(8)の場合、2を何乗したら8になるかを計算し、出力は3となります。
import matplotlib.pyplot as plt
import numpy as np
import math
x = np.arange(0.1, 4, 0.1)
y = np.log(x)
plt.plot(x, y, label="")
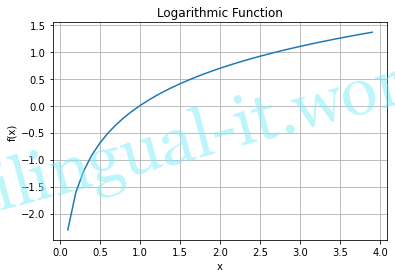
plt.title("Logarithmic Function")
plt.ylabel("f(x)")
plt.xlabel("x")
plt.grid()
plt.show